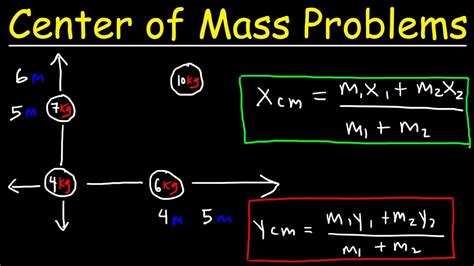
find the center of mass for a metal l bracket Learning Objectives. Find the center of mass of objects distributed along a line. Locate the center of mass of a thin plate. Use symmetry to help locate the centroid of a thin plate. Apply the theorem of Pappus for volume. . $7.99
0 · Physics 201 Lab 8: Finding the Center of Mass
1 · Moment of Inertia of an L
2 · L07
3 · Finding the center of mass
4 · Center of Mass Calculator
5 · 9.6 Center of Mass
6 · 6.6: Moments and Centers of Mass
7 · 22A: Center of Mass, Moment of Inertia
8 · 2.7.24: Calculating Centers of Mass and Moments of
9 · 15.6: Calculating Centers of Mass and Moments of
The fuel pump relay for the 2003 f350, is an integral part of the central junction block(fuse box) located under the left side of the dash. So in order to replace the relay, you would have to .
Find the center of mass vector Rcm of the entire bracket using the origin O which is at the center of the middle square. Find numerical values for fractions f and f’ in the expression: Rcm = f L i + f’ L j. From your results, draw the center of mass point on the drawing.
In this section we develop computational techniques for finding the center of mass and moments of inertia of several types of physical objects, using double integrals for a lamina (flat plate) and triple integrals for a three .
The point where all three lines intersect is the center of mass of the L-bracket. Note that the center of mass coordinate of a body need not lie within the body itself. Summary Procedure
Learning Objectives. Find the center of mass of objects distributed along a line. Locate the center of mass of a thin plate. Use symmetry to help locate the centroid of a thin plate. Apply the theorem of Pappus for volume. .A uniform thin bar formed into a L-shaped object of mass $m=2.5kg$ with a longer side of length $l=0.8m$ and a shorter side of length $l/2$. Initially the . Find the position of the center of mass of a thin rod that extends from \(0\) to \(.890\)m along the \(x\) axis of a Cartesian coordinate system and has a linear density given by \(\mu(x)=0.650\frac{kg}{m^3}x^2\). SolutionFind the center of mass of a uniform thin hoop (or ring) of mass M and radius r. Strategy First, the hoop’s symmetry suggests the center of mass should be at its geometric center.
To calculate the center of mass of a triangle with this tool, enter the coordinates of the points of the triangle and make sure that the masses are all the same (the specific mass value doesn't matter). Also, you can simply use our . Find the center of mass of objects distributed along a line. Locate the center of mass of a thin plate. Use symmetry to help locate the centroid of a thin plate. Apply the theorem of Pappus for volume.
What we're seeing is a very general and powerful rule that applies to calculating the center of mass: if we have two equal masses \(m_1 = m_2\) at exactly opposite positions, \(\vec{r}_1 = -\vec{r}_2\), then their total contribution to the .Question: Find the location of the centre of mass of the bracket-and-shaft combination shown below,relative to the x,y and z axes shown.Mass of the sheet metal used for vertical face =30kgm2Mass of horizontal base material =30kgm2Density of metal used for shaft =2700kgm350 mm given at the top of the figure is the radius of the .Question: Determine the coordinates of the mass center of the bracket, which is constructed from sheet metal of uniform thickness. Show transcribed image text. There’s just one step to solve this. Solution. Answered by. Mechanical .
scipy.ndimage.measurements.center_of_mass seems to be the right thing, but unfortunately, the function always returns two values (instead of 3). In addition, I can't find any documentation on how to set up an ndimage from an array: Would I use a numpy array N of shape (9,4)? Would then N[:,0] be the x-coordinate?Engineering; Mechanical Engineering; Mechanical Engineering questions and answers; Determine the coordinates of the center of mass of Determine the coordinates of the mass center of the the bracket, which is made from a plate of uniform bracket, which is constructed from sheet metal of thickness. uniform thickness. 40 mm 80 mm 3" 80 mm 100 mmDetermine the x-coordinate of the mass center of the bracket constructed of a uniform steel plate. Assume that the bracket shown is made from a homogeneous . flat plate of negligible thickness. What are the x and Z coordinates of the brackets mass center? Locate the center of mass (\bar x , \bar y , \bar z ) of the homogeneous block assembly.Question: Determine the coordinates of the mass center of the bracket, which is constructed from sheet metal of uniform thickness. Answer: (Xˉ,Yˉ,Zˉ)=(,, in. Show transcribed image text. There’s just one step to solve this. Solution.
metal fabrication battle creek mi
A fun center-of-mass experiment that you can perform at home involves using a simple technique for finding the center of mass of a broom. All you need for this experiment is one broom and two hands. With your hands relatively far apart, hold up the broom on the end of two pointer fingers. Then, slowly bring your hands closer together, sliding . In summary, the conversation was about finding the center of mass of a cubical box made of uniform metal plate. The box had an open top and an edge length of 40cm. The professor used a method involving mass moments, where the x, y, and z components for the center of mass were found first.
hanging from the pivot point. The point where all three lines intersect is the center of mass of the L-bracket. Note that the center of mass coordinate of a body need not lie within the body itself. Summary Procedure 1. Tape a sheet of paper into the inside corner of the L-bracket, as shown in gure 2. 2. For each of the three possible pivot points:
Find the location of the centre of mass of the bracket-and-shaft combination shown below, relative to the x, y and z axes shown. Mass of the sheet metal used for vertical face = 20 kg / m 2 Mass of horizontal base material = 30 kg / m 2 Density of metal used for shaft = 2700 kg / m 3 50 mm given at the top of the figure is the radius of the semicircular shape on the vertical face.
metal fabrication background
Find the location of the centre of mass of the bracket-and-shaft combination shown below, relative to the x, y and z axes shown. 150 mm 75 mm 50 mm 25 mm 100 mm 50 mm Z 50 mm 150 mm -40 mm 150 mm y 3 4 Mass of the sheet metal used for vertical face = 25 kg/m² Mass of horizontal base material = 30 kg/m² Density of metal used for shaft = 7850 kg/m³ 50 mm given at the top .1. Finding the Momcnt of Inertia of a Uniform Thin Rod with mass M and length L rotating about its center (a thin rod is a 1D object; in the figure the rod has a thickness for clarity) For this problem, usc a coordinate axis with its origin at the rod's center and let the rod cxtend along the x axis as shown here (in other problems, you will nced to gencrate the diagram) dx dm Now, we select a .L-bracket from each of three pivot points. In each case, you will trace a vertical line along a plumb bob hanging from the pivot point. The point where all three lines intersect is the center of mass of the L-bracket. Note that the center of mass coordinate of a body need not lie within the body itself. Summary Procedure 1. Determine the coordinates ofthe center of mass of the bracket,which is made from a plate ofuniform thickness.
Question: Determine the coordinates of the mass center of the bracket, which is constructed from sheet metal of uniform thickness. Answer: (X,Y,Z) 2.7" = IN 3.8" Z 1.0" 1.9" i 4.7" 2.7" Mi ) in. Determine the coordinates of the mass center of .Determine the x coordinate of the mass center of the bracket constructed of uniform steel plate. Determine the x-coordinate of the mass center of the bracket constructed of a uniform steel plate. Calculate the \bar x, \bar y, and \bar z . The shape and size of the bracket can affect the required steel thickness. Larger and more complex brackets may require thicker steel to withstand the forces applied to them. Additionally, the shape of the bracket can also impact the distribution of stress and may require a thicker steel in certain areas. 5.Question: use the procedure to find the centre of mass of a composite body to Find the location of the centre of mass of the bracket-and-shaft combination shown below,relative to the x,y and z axes shown.Mass of the sheet metal used for vertical face =30kgm2Mass of horizontal base material =40kgm2Density of metal used for shaft =7850kgm350 mm .
Physics 201 Lab 8: Finding the Center of Mass
Find the location of the centre of mass of the bracket-and-shaft combination shown below, relative to the x, y and z axes shown. 50 mm 150 mm 150 mm 75 mm 25 mm 100mm 150 mm Mass of the sheet metal used for vertical face=30 kg/m2 Mass of horizontal base material = 40 kg/m2 Density of metal used for shaft = 2700 kg/m3 50 mm given at the top of the figure is .Question: Determine the coordinates of the mass center of the bracket, which is constructed from sheet metal of uniform thickness. 4.8 4.3" 3.2" 204 24 Answer: 3.40 3.12 -1.31 (X.7.Z) in. Show transcribed image text
Example Problem # 8: Locate the center of mass (X,Y,Z) of the bracket-and-shaft combination. The vertical face is made from a sheet metal with a mass density of 25 kg/m2. The sheet metal material of the horizontal base has a mass density of 40 kg/m2. Neglect the thickness of all sheet metal components. The steel shaft has a mass density of 7.83 .The uniform beam is 1 m long with center of mass at its geometric center. The sign is centered and is .8 m lo; The sign has a mass of 60 kg with center of mass at G. Determine the x, y, z components of reaction at the ball-and-socket joint A and determine the . 1 1/8" thick metal would need an entire high rise building to sit on it to bend it. do you know a metal shop that can make the bracket that you need? Reactions: . I thought you had an L bracket from an Abrams tank turret for a minute there. .x = L / 2 x = L/2 x = L /2. This means that the x-coordinate of the mass centre of the bracket is the same as the centroid: x = L / 2 x = L/2 x = L /2. We have to be careful because this will only be true for the brackets that have both L L L and H H H the same dimensions.
Question: Find the location of the centre of mass of the bracket-and-shaft combination shown below,relative to the x,y and z axes shown.Mass of the sheet metal used for vertical face =30kgm2Mass of horizontal base material =40kgm2Density of metal used for shaft =7850kgm350 mm given at the top of the figure is the radius of the .Determine the position of the mass center of the cylindrical shell with a closed semicircular end. The shell is made from sheet metal with a mass of 24 k g / m 2 24 \mathrm{~kg} / \mathrm{m}^2 24 kg / m 2, and the end is made from metal plate with a mass of 36 k g / m 2 36 \mathrm{~kg} / \mathrm{m}^2 36 kg / m 2.Question: Find the location of the centre of mass of the bracket-and-shaft combination shown below, relative to the x,y and z axes shown. Mass of the sheet metal used for vertical face =25 kg/m2 Mass of horizontal base material =40 kg/m2 Density of metal used for shaft =7850 kg/m3 50 mm given at the top of the figure is the radius of the semicircular shape on the
Moment of Inertia of an L
metal fabrication australia
We would like to show you a description here but the site won’t allow us.
find the center of mass for a metal l bracket|2.7.24: Calculating Centers of Mass and Moments of