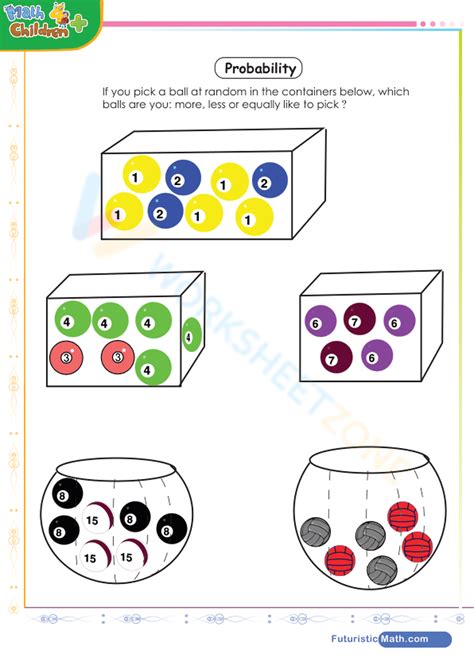
distribute n balls of m colours in r boxes I want to distribute n labeled balls into m labeled boxes. I know one obtains the . Although, in article 314.17(C)'s exception, nonmetallic boxes have no cable clamps and must have cables supported within eight inches of the junction box. In either instance, the wire is secured by wire staples that keep it from moving within the wall cavity.
0 · probability n balls m boxes
1 · n balls vs m boxes
2 · m balls on n boxes
3 · indistinguishable balls on n boxes
4 · how to distribute n boxes
5 · how to distribute m on n
6 · how to distribute k balls into boxes
7 · distributing balls to boxes
If you use a metal box instead of a plastic one, you can bring the wire in through the knockout on the back of the box. You can get a cable gland (cable grip with a rubber grommet that tightens around the wire) for NM cable — the box stores have these.
Admittedly there are $$\binom{N+m-1}{N}=\dfrac{(N+m-1)!}{N!(m-1)!}$$ ways to distribute $N$ indistinguishable balls in $m$ boxes, but each way does not occur with the same probability. .I want to distribute n labeled balls into m labeled boxes. I know one obtains the .distribute k indistinguishable balls into n distinguishable boxes, without exclusion. We should discuss another condition that is commonly placed on the distribution of balls into boxes, .
custom machined sheet metal parts
Through some research I found that the answer is $\Omega = \binom{M+N-1}{N-1}$ But why? I found an explanation which explained it like this: Let the balls be $\circ$. To find out how the . Distribute $a + b + c$ distinct balls into boxes $A, B, C$ such that $a$ balls, $b$ balls and $c$ balls go to boxes $A, B, C$ Given an array arr[] of size N, representing the number of balls of each of N distinct colors, the task is to find the probability of distributing all the balls into two boxes, such . The multinomial coefficient gives you the number of ways to order identical balls between baskets when grouped into a specific grouping (for example, 4 balls grouped into 3, 1, .
Let's say you have a group of M M balls of different colors in a box. For example, 20 balls are red, 15 are blue, 10 are green, 5 are grey, 5 are yellow and 5 violet, for a total of M .
Probability of a Two Boxes Having The Same Number of Distinct Balls - Given 2n balls of k distinct colors. You will be given an integer array balls of size k where balls [i] is the number of . I want to distribute n labeled balls into m labeled boxes. I know one obtains the number by $m^n$. But I don't quite understand why. The underlying argument is always I have .When distributing n indistinguishable balls into m distinguishable boxes, the total number of ways can be calculated using the formula: $$C(n + m - 1, m - 1)$$. If each box can hold any number .
Admittedly there are $$\binom{N+m-1}{N}=\dfrac{(N+m-1)!}{N!(m-1)!}$$ ways to distribute $N$ indistinguishable balls in $m$ boxes, but each way does not occur with the same probability. For example, one way is that all $N$ balls land in one box.distribute k indistinguishable balls into n distinguishable boxes, without exclusion. We should discuss another condition that is commonly placed on the distribution of balls into boxes, namely, the condition that no box be empty.Through some research I found that the answer is $\Omega = \binom{M+N-1}{N-1}$ But why? I found an explanation which explained it like this: Let the balls be $\circ$. To find out how the balls are distributed in the boxes we use $N-1$ "|". Distribute $a + b + c$ distinct balls into boxes $A, B, C$ such that $a$ balls, $b$ balls and $c$ balls go to boxes $A, B, C$
Given an array arr[] of size N, representing the number of balls of each of N distinct colors, the task is to find the probability of distributing all the balls into two boxes, such that both the boxes contain an equal number of distinct colored balls.
The multinomial coefficient gives you the number of ways to order identical balls between baskets when grouped into a specific grouping (for example, 4 balls grouped into 3, 1, and 1 - in this case M=4 and N=3). Let's say you have a group of M M balls of different colors in a box. For example, 20 balls are red, 15 are blue, 10 are green, 5 are grey, 5 are yellow and 5 violet, for a total of M = 60 M = 60 balls. You pick 1 ⩽ n ⩽ M 1 ⩽ n ⩽ M of them without replacement.Probability of a Two Boxes Having The Same Number of Distinct Balls - Given 2n balls of k distinct colors. You will be given an integer array balls of size k where balls [i] is the number of balls of color i.
I want to distribute n labeled balls into m labeled boxes. I know one obtains the number by $m^n$. But I don't quite understand why. The underlying argument is always I have m choices for the first ball m choices for the second and so on. As an example lets take 3 balls labeled A,B,C and two boxes 1,2
When distributing n indistinguishable balls into m distinguishable boxes, the total number of ways can be calculated using the formula: $$C(n + m - 1, m - 1)$$. If each box can hold any number of balls (including zero), this scenario fits perfectly within the framework of .Admittedly there are $$\binom{N+m-1}{N}=\dfrac{(N+m-1)!}{N!(m-1)!}$$ ways to distribute $N$ indistinguishable balls in $m$ boxes, but each way does not occur with the same probability. For example, one way is that all $N$ balls land in one box.
distribute k indistinguishable balls into n distinguishable boxes, without exclusion. We should discuss another condition that is commonly placed on the distribution of balls into boxes, namely, the condition that no box be empty.Through some research I found that the answer is $\Omega = \binom{M+N-1}{N-1}$ But why? I found an explanation which explained it like this: Let the balls be $\circ$. To find out how the balls are distributed in the boxes we use $N-1$ "|". Distribute $a + b + c$ distinct balls into boxes $A, B, C$ such that $a$ balls, $b$ balls and $c$ balls go to boxes $A, B, C$ Given an array arr[] of size N, representing the number of balls of each of N distinct colors, the task is to find the probability of distributing all the balls into two boxes, such that both the boxes contain an equal number of distinct colored balls.
The multinomial coefficient gives you the number of ways to order identical balls between baskets when grouped into a specific grouping (for example, 4 balls grouped into 3, 1, and 1 - in this case M=4 and N=3). Let's say you have a group of M M balls of different colors in a box. For example, 20 balls are red, 15 are blue, 10 are green, 5 are grey, 5 are yellow and 5 violet, for a total of M = 60 M = 60 balls. You pick 1 ⩽ n ⩽ M 1 ⩽ n ⩽ M of them without replacement.Probability of a Two Boxes Having The Same Number of Distinct Balls - Given 2n balls of k distinct colors. You will be given an integer array balls of size k where balls [i] is the number of balls of color i. I want to distribute n labeled balls into m labeled boxes. I know one obtains the number by $m^n$. But I don't quite understand why. The underlying argument is always I have m choices for the first ball m choices for the second and so on. As an example lets take 3 balls labeled A,B,C and two boxes 1,2
custom metal enclosure services
probability n balls m boxes
custom made metal fabrication sidney oh
n balls vs m boxes
m balls on n boxes
I was replacing a receptacle in my home and noticed that the cable into the box did not have a clamp. Is there an easy way to install something from inside the box to protect the cable without having to cut into the drywall around the box?
distribute n balls of m colours in r boxes|indistinguishable balls on n boxes